Skew

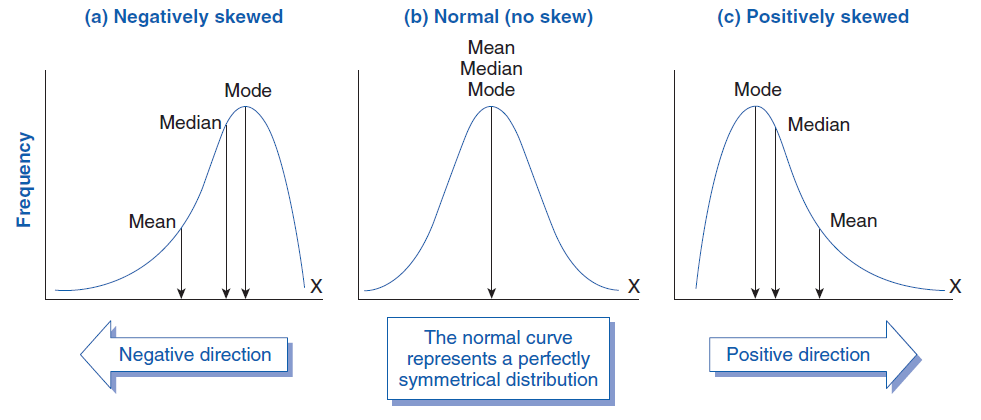
Skewness is a measure of the asymmetry of the distribution of the measurements of a variable relative to its mean.  As the data becomes skewed from a normal distribution, the mean loses its ability to provide the best measure of central tendency.

​As the data becomes skewed from a normal distribution, the mean loses its ability to provide the best measure of central tendency.

How to I know if my data is skewed?

You’ll calculate skew for the trials for each level of your manipulated variable.  So, if you had five levels of manipulation, you’ll calculate skew 5 times - one time each with the data for each level of your manipulated variable.

• Use an online SKEW calculator.  Here’s a good option.  Be sure to include a citation in your paper if you use this tool.  
• Use the “SKEW” function in Microsoft Excel. Here’s directions.  
• Use the “SKEW” function in Google Sheets.  Here’s the directions.

The result of the SKEW test is a number between -1 and 1.  If the skew value is negative, then your data is negatively skewed.  If the skew value is positive, then your data is positively skewed.  

The absolute value of the number indicates just how skewed the data is.  If skewness = 0, the data are perfectly symmetrical. But a skewness of exactly zero is quite unlikely for real-world data, so how can you interpret the skewness number? Bulmer (Bulmer, M. G. 1979. Principles of Statistics. Dover) suggests this rule of thumb:

• If skewness is less than −1 or greater than +1, the distribution is highly skewed.
• If skewness is between −1 and −.5 or between +.5 and +1, the distribution is moderately skewed.
• If skewness is between −.5 and +.5, the distribution is approximately symmetrical.

Any absolute value 1.0 or less is fine for using the mean as your measure of central tendency.  If the absolute value is more than 1.0, consider using the median to represent your data.